차원 분석이란 기본적으로 다수의 데이터로 인해 의미 있는 무언가를 뽑아내기 어려운 경우 데이터의 차원을 축소하는 방식으로 사용하게 된다. 데이터의 차원을 축소하는 이유는 데이터셋에 많은 변수가 포함되는 경우 분석의 복잡성이 증가하고, 이로부터 의미있는 정보를 찾기에 어려움이 생기 때문이다. 이런 경우 데이터셋에 포함된 여러 변수를 소수의 해석 가능한 변수로 축소할 필요가 있다. 주성분분석(Principal Component Analysis), 요인분석(Factor Analysis), 다차원 척도법(Multidimensional Scaling) 등은 데이터의 차원을 줄여주어 데이터의 복잡성을 감소시킨다.
1. 주성분 분석
- 서로 상관관계를 갖는 많은 변수를 상관관계가 없는 소수의 변수로 변환하는 차원축소 기법
- 이때 변환에 사용하는 소수의 변수를 주성분(Principal Component) 또는 성분(Component)라 함
- 주성분 분석의 수식은 아래와 같음

- 위의 식을 해석해보면, PC는 주성분으로 기존 변수들의 선형결합으로 표현되며, 기존 변수에 대한 가중치는 주성분 간 상관관계가 없으면서 각 주성분이 설명하는 분산(여기서 분석이란, 변수가 가지고 있는 정보(information))이 최대가 되도록 결정함
- 이론적으로 n개의 변수가 있을 때 n개의 주성분을 생성하면, 본래의 총분산과 같은 값이 나오게 됨. 하지만 이 경우 주성분 분석을 통해 변수를 축소하는 것의 의미가 없으므로, 주성분 분석에서는 추출된 주성분 중 일정 Criteria(기준점)을 만족시킬 정도로 설정함.
- PCA는 기본적으로 연속형 변수에 대해서만 진행이 가능함(PCA에 기본 개념 또한 연속형 변수임을 가정하고 있음). 다만 필요한 경우 범주형 변수에 대해서는 가변수화(dummy화)를 통해서 가능함(추천하지는 않음 - 관련 논의 : https://stackoverflow.com/questions/40795141/pca-for-categorical-features).
- 코드 작성
str(state.x77) # R 기본 패키지에 포함되어 있는 데이터셋
#PCA를 수행하는 함수 : prcomp
# 코드 관련 설명 : https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/prcomp
pca <- prcomp(state.x77, #PCA를 수행할 데이터
scale = T #표준화 진행
)
summary(pca)이를 실행하면 아래와 같은 결과를 얻을 수 있음.

- 위의 결과를 해석해보면, 첫 번째 Principal Component로 약 0.45 정도의 정보에 대해 설명할 수 있고, 두 번째 Principal Component로는 약 0.2 정도의 정보를 설명할 수 있음(이에 따라 Cumulative Proportion이 두 번째 Principal Component에서 0.65 정도임)
이를 시각화해서 확인해보면 다음과 같음.
plot(pca, #앞서 생성한 PCA
type = "l", # line 그래프 그리기
col = "blue", # 선의 색깔
main = "Scree Plot")
이를 통해 확인해보면, 두 번째 Principal Component에서 비교적 큰 꺾임이 일어나는 것을 알 수 있음. 이런 방식으로도 확인할 수 있으며, 최소 일정량 이상의 정보를 설명해야한다는 식으로도 생각해볼 수 있음(cumulative proportion이 0.8 이상인 지점까지의 변수를 사용한다 등)
- 이후 변수와 Principal Component 사이의 관계는 앞서 생성한 pca에서 rotation항목에 저장되어 있으며 이를 확인하는 건 아래와 같음.
round(pca$rotation, 3) #소수점 셋째자리까지 보여주기. 이를 지정하지 않으면, 소수점이 나타나지 않아서 어려움이 있음.
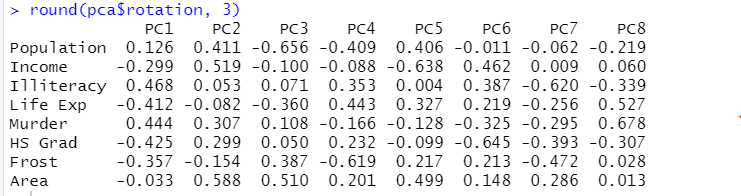
위의 결과를 토대로 Principal Component가 어떻게 생성되었는지 파악할 수 있음. 예를 들어 PC1같은 경우 PC1에 해당하는 열의 결과(성분적재값)가 다 더해진 값임.
위에서 변수들의 선형결합을 통해 변환된 값을 성분점수(Component Score)라 함. 이는 위에서 나타난 성분적재값을 변수값에 곱하고 이를 합산하여 나타남. 이를 구하는 것은 아래와 같음.
round(scale(state.x77) %*% pca$rotation, 3)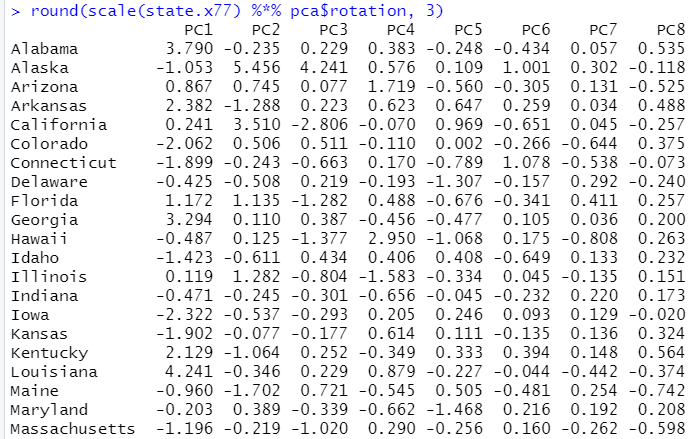
지면 관계상 이 정도에서 짤랐지만, 해당 데이터는 50개 주에 대한 정보이기 때문에 각각의 주에 대한 계산값이 소수점 셋째 자리까지 표현되게 됨.
이는 함수 자체에서 제공하는 값을 통해서 확인할 수 있음.
round(pca$x, 3)앞서 언급한 바와 같이 모든 주성분을 활용할 필요는 없음.
따라서 만약 두 번째 주성분까지만 활용한다고 생각했으면 아래와 같이 해서 성분점수를 계산해볼 수 있음.
round(pca$x[,c(1,2)],3)위의 결과를 토대로 PCA를 시각화하여 표현해볼 수 있음. 흔히 사용하는 PCA에 대한 시각화는 biplot을 사용함

- 위에서 붉은 색으로 표현된 것은 변수임. 이때 직각 관계에 있는 건 상관관계가 없음/ 비슷하게 뻗어나가는 건 양의 상관관계, 반대방향으로 되어 있는 건 음의 상관관계를 갖는다는 의미임.
- PCA는 이와 같이 사용될 수 있으며, 설문조사와 같은 주관적인 정보에 대해서도 수행할 수 있음. 이를 토대로 여러가지의 설문 항목 중 비슷한 결과값을 나타내는 설문항목을 묶어서 하나의 Principal Component로 나타낼 수도 있으며, 두 가지의 상위 PC를 토대로 행렬도를 그릴 수도 있음. 이렇게 그려진 행렬도를 Perceptual map(지각도)라 함.
2. 요인 분석(Factor Analysis)
- 요인 분석은 관측 가능한 여러 변수로부터 소수의 Factor를 추출하여 이러한 Factor를 토대로 변수 간의 관련성을 설명하려는 데이터 분석 기법임.
- 예를 들어 전교생의 국어, 영어, 한문, 수학, 물리, 화학 점수는 언어능력(국어, 영어, 한문) 및 수리능력(수학, 화학, 물리)으로 분리하여 측정할 수 있음. (이때 언어능력과, 수리능력은 실제로는 관측되지 않았지만, 공통의 Factor라 볼 수 있음)
- 즉, 서로 상관관계를 맺고 있어서 직접적으로 해석하기 어려운, 여러 관찰(측정)변수들 간의 구조적 연관관계를 상대적으로 독립적이면서, 변수들의 저변구조를 이해하기 위해 개념상 의미를 부여할 수 있는 원래 변수들의 갯수보다 훨씬 적은 갯수의 공통인자(Common Factor/잠재변수(latent variable)를 상정하여, 이들을 통해 분석하고자 하는 통계적 방법임. (좀 더 통계적으로 생각해보면, 상관(혹은 공분산) 행렬의 구조에 관한 통계적 모형을 구축하고, 그와 같은 구조를 생성시키는 소수 몇 가지의 인자를 유도하여 변수들 간의 구조적 관계를 해석하는 공분산 내지 상관 중심의 기법임.
- 주성분 분석(PCA)와 유사한 듯 보이나, 실질적으로 요인 분석의 목적은 측정 가능한 변수들로부터 해석 가능한 소수의 요인을 찾기 위함(이를 위해 Factor의 축을 rotate시키는 방식을 사용함).
- 본 분석을 위해 kaggle을 통해 설문조사 데이터를 가져옴(https://www.kaggle.com/datasets/ipravin/hair-customer-survey-data-for-100-customers)
- Step 1 : 요인의 갯수 정하기(해당 데이터가 몇 가지 정도의 Factor를 사용하는 게 좋을지- 단, 일반적으로 해석을 위해서는 2개의 Factor를 사용하기는 함)
일반적으로 아래 3가지를 기준으로 사용하게 됨.
1) 고유값(eigenvalue, 요인이 설명하는 분산의 양을 나타냄)를 사용하는 것 -> 1보다 큰 고유값을 갖는 요인의 갯수만큼 추출하는 것 (1보다 작을 경우 새로 추출한 요인에 의해 설명되는 분산이 기존 변수 1개의 분산에도 못 미치기 때문)
2) 스크리 도표 활용 -> 급격한 경사 이후 완만한 경사를 나타내는 지점에서 끊기
3) 원래의 데이터셋과 동일한 표본크기를 갖는 무작위 데이터 행렬로부터 고유값을 추출하는 방식으로 시뮬레이션 수행(계산한 고유값의 평균보다 큰 지점에서 요인의 갯수를 선택함)
이를 코드로 계산해보기
#데이터 불러오기
survey<- fread("Factor-Hair-Revised.csv")
survey<-as.data.frame(survey)
#필요 패키지 불러오기
library(psych)
library(nFactors)
# 추출할 요인의 갯수 지정하기(fa.parallel 함수 활용)
fa.parallel(survey, #데이터 프레임
fm = "ml", # 최대우도법(Maximum Likelihood)를 토대로 요인의 갯수 지정
fa = "fa", # 요인분석(Factor Analysis)를 위한 고유값 표기
n.iter = 100 # 반복 횟수
)
# 4개를 사용하는 것을 추천
# 다른 방법(nFactor 패키지 활용)
nScree(survey)
# 4가지 방법론 중 3가지에서 4개의 Factor을 추천
# 다른 방법 eigen value 확인
eigen(cor(survey))
# eigen value가 1을 넘는 것이 4번째까지임.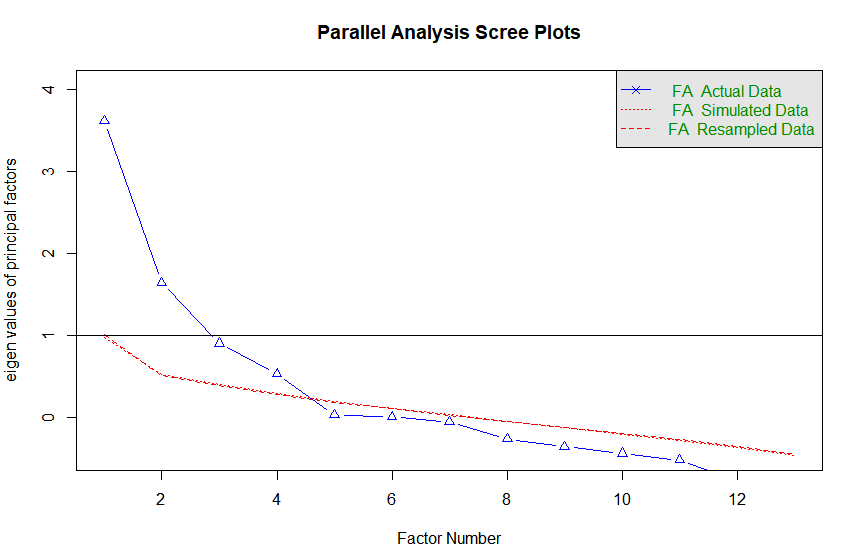
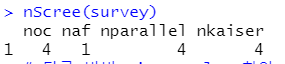

다만, 이러한 결과는 보조 수단일뿐이며, 실제 선택은 '해석 가능성'에 조금 더 초점을 맞춰야 함. (우선 현재 분석에서는 따로 해석의 목적이 없으므로 요인 갯수를 위에서 제시한 4개로 분석)
- Factor Analysis 코드
#요인 분석 수행하기
fa <- factanal(survey, # 데이터
factor = 4, #요인의 갯수
scores = "regression") #요인점수 계산 시 사용할 방법 지정
fa해당 코드에 대한 결과는 아래와 같음

이를 해석해보면
1) Uniquenesses는 고유분산(uniqueness or specific variance)을 의미함
→ '1 - 고유분산'이 공통성(communality or common variance)이 되므로 각 변수의 공통성을 계산할 수 있음
→ 공통성이란 공통요인에 의해 설명되는 분산의 비율이며 1~0의 값을 가짐. 이때 공통성이 1이면 공통요인이 변수의 분산을 완전히 설명한다는 것이며, 0이면 하나도 설명하지 못한다는 것임(공통요인에 의해 설명되지 않는다는 건 고유요인에 의해 의해 설명될 수 있다는 것이며, 이에 따라 공통성이 크면 클수록 요인 추출이 성공적으로 이루어진 것임. )
→ 대략적으로 0.5이하면 유효함 (독립변수로 사용이 가능하다)
→ 현재 위의 결과상으로는 ID 및 Advertising의 경우 독립변수로의 사용 X (제외하고 재분석해보는 방법도 가능)
→ 만약 설문지에 대한 값을 분석하는 것이라면, 특정 문항의 질문이 다른 질문지와의 align가 맞지 않다고 이야기할 수도 있음.
2) loadings
→ 해당 영역을 통해 각 변수을 Factor 값으로 표현할 수 있음.
→ 예를 들어 Satisfaction = 0.519* Factor1 + 0.482*Factor2 + 0.594*Factor3 + e1 임
→ 또한 이를 통해 각 Factor가 어떤 변수에 높은 영향을 받는지 파악할 수 있음. 예를 들어 Factor 3의 경우 TechSup 및 WrantyClaim의 값이 높은 것과 관련이 높음.
3) loadings 다음 영역
→ SS loadings : 각 변수가 가지는 가중치 (ex. Factor 1이 가장 가중치가 높다)
→ Proportion Var : 분산
→ Cumulative Var : 누적
4)
Test of the hypothesis that 4 factors are sufficient.
The chi square statistic is 49.13 on 32 degrees of freedom.
The p-value is 0.027
영역 : 우리가 지정한 Factor의 갯수가 충분한지에 대한 Test. 이때는
귀무가설 : 현재의 모형이 충분하다
대립가설 : 현재의 모형이 충분하지 못하다. 이다
이때 P-value의 값이 0.05 이하이므로 귀무가설을 기각하여 Factor 갯수가 충분하지 않음을 알 수 있음.
※ 참고 : 만약 Factor의 갯수를 정하기 어렵다면, Factor Analysis 자체가 해석에 주안점을 두고 있기 때문에 해석을 보고 판단하도록 한다.(ex. 해석을 위해 2개 정도로 줄임 등)
Factor analysis에서 변수간의 상관관계는 공통요인을 공유하기 때문이라고 가정함. 따라서 Factor analysis에서 추출한 공통요인을 바탕으로 변수 간의 상관관계를 재현할 수 있다면 실제 관측된 상관관계와 재현된 상관관계를 비교함으로써 요인분석의 적정성을 평가할 수 있음(둘 사이의 차이가 작을수록 재현이 잘 된 것). 이를 코드로 표현해보면 아래와 같음.
#요인 분석의 결과를 토대로 상관관계 파악하기
round(cor(survey) - #기존값에 대한 실제 상관관계 파악
(fa$loadings %*% t(fa$loadings) + #요인분석 결과의 loading과 요인분석 결과의 transpose의 행렬곱
diag(fa$uniquenesses)), #diag 함수는 주어진 벡터로 대각선을 채우고 나머지는 다 0으로 채움.
#이때 fa$uniqueness는 각 변수의 고유분산을 의미함
3) # 소수점 셋째 자리까지 표현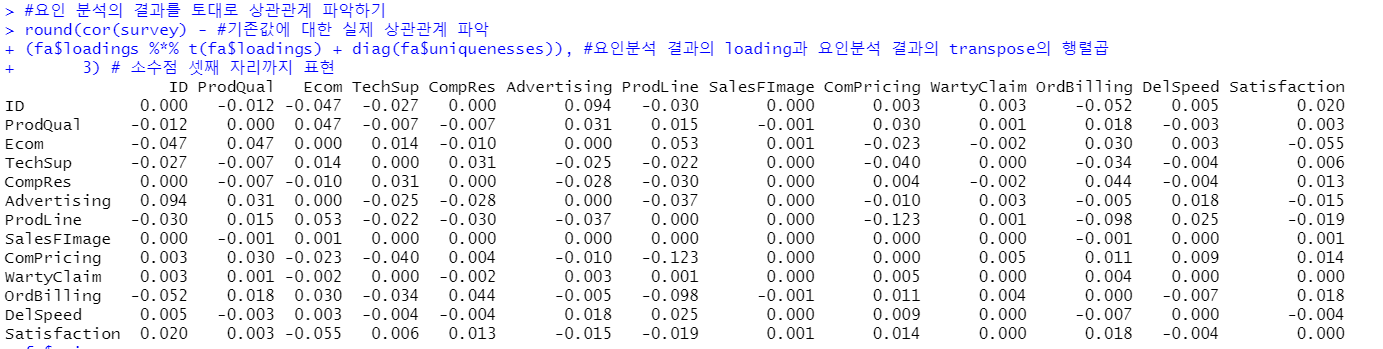
위의 결과를 해석해보면, 이는 각 변수간 잔차의 차이임. 예를 들어 ID와 ProdQual의 경우 잔차의 차이가 -0.012라는 뜻임. 즉, 잔차가 크면 추출한 요인과 데이터 간의 적합도가 좋지 않다는 것을 나타냄. 현재 대부분의 변수가 0에 가깝기 때문에 추출이 잘 이루어졌다고 할 수 있음.
이제는 그림을 통해 각 Factor 및 변수의 관계를 파악해볼 수 있음.
#Factor Plot 그리기
factor.plot(fa, labels = colnames(survey), pch = 20, pos= 4,
title= "Factor Plot")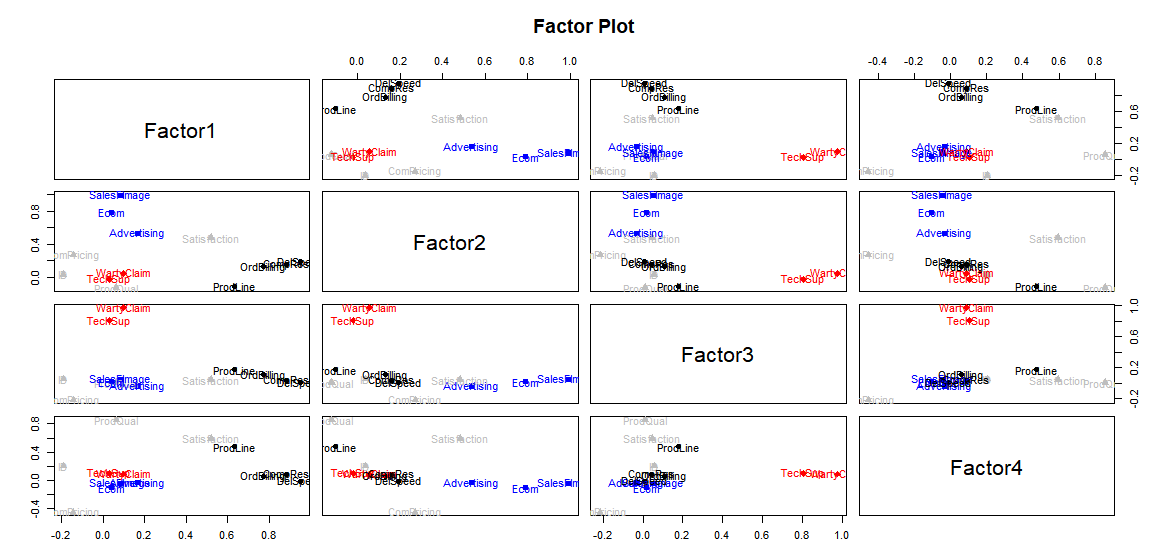
이외에도 여러가지 시각화를 통해 확인하는 방법들이 있음. 예를 들어 gplots, RColorBrewer 패키지 내 heatmaps.2를 통해 히트맵으로 나타내는 방법이나, semPlot 패키지 내 semPaths 함수를 토대로 경로도를 그리는 방법 등이 있으나 여기서는 semPlot 패키지를 통해 SemPaths 함수를 사용하는 방법으로 시각하를 진행해봄.
#경로도 (Path Diagram 그리기)
#참고 : semPlot 패키지가 생각보다 무거워서 시간이 오래걸림.
library(semPlot)
semPath(fa, what = "est", # 경로상에 요인적재값 나타내기
residuals = F, # 관측변수의 잔차 생략
cut = 0.3, # 0.3보다 작은 요인적재값은 그래프상에 나타나지 않도록 함
posCol = c("White", "darkgreen"), # 양수 관련
negCol = c("white", "red"), # 음수 관련
edge.label.cex = 0.75) # 요인적재값의 텍스트 크기이에 대한 결과는 아래와 같다.
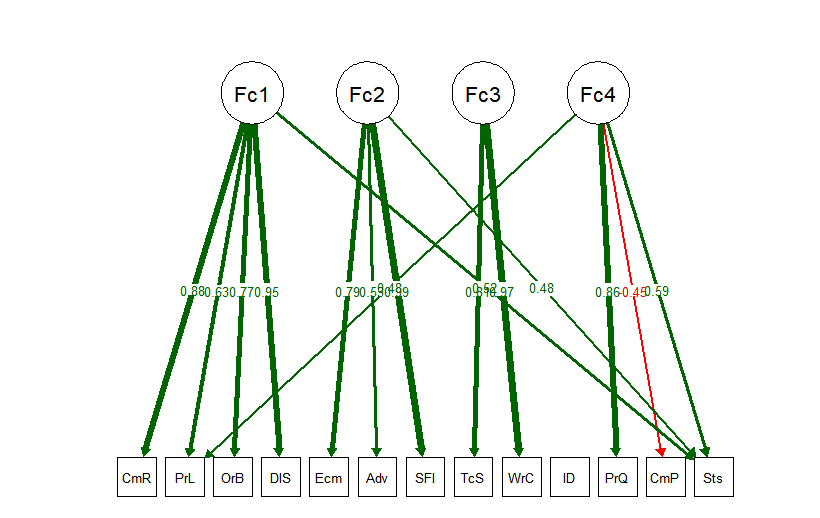
※ 참고 : 학계에서는 Factor Analysis를 통해 확증적 인자분석(Confirmatory Factor Analysis)를 진행하기도 함. 이는 구조를 가정하고 하는 것으로 내 모델이 얼마나 make Sense 한지, 이론에 데이터가 맞는지를 검증하기 위해 사용 (ex. 국어, 영어, 한문, 수학, 화학, 물리 시험 점수가 있는 경우, 국어, 영어, 한문이 언어능력, 수학, 화학 물리 수리 능력과 관련이 있다고 가정하고 분석 진행)
3. 다차원 척도법(Mutidimensional Scaling, MDS)
- 다차원 척도법은 케이스 간의 거리 정보를 토대로 이들 간의 관계를 시각적으로 표현하는 기법임. 여기서 거리는 연속형 변수가 주어지는 경우 물리적인 거리를 의미할 수도 있고(유클리드 거리), 범주형 변수까지 포함되어 있는 경우 비계량적 거리 측정법(gower 거리를 구하기 위해 daisy 함수를 사용) 할 수 있음.
- 우선 연속형 변수만 있는 경우 MDS의 기초 예시 중 하나인 판사의 평가 점수를 기록한 USJudgeRatings 데이터를 사용(내장되어 있는 기본 데이터)
#다차원 척도법 MDS
# case 1 : 연속형 변수만 있는 경우
# 해당 데이터는 행의 이름에 판사의 이름이 들어가 있는 구조임(아래 plotting에서 사용)
str(USJudgeRatings)
# 연속형 변수이므로 우선 거리를 계산해야 함.
# 이후 계량 데이터로부터 생성된 근접행렬에 대해 적용할 수 있는 cmdscale()함수를 이용하여 MDS 수행
usjudge_dist <- dist(USJudgeRatings) # 유클리드 거리계산
usjudge_mds <- cmdscale(usjudge_dist)
# 이후 이에 대한 결과는 plot() 함수와 text() 함수를 이용하여 MDS 공간배치도로 나타낼 수 있음.
plot(usjudge_mds, type = 'n',
main = "다차원척도법 스케일 플롯") # 비어있는 플롯을 생성
text(usjudge_mds, rownames(USJudgeRatings), col = "red", cex = 0.6)이에 대한 결과는 아래와 같음.
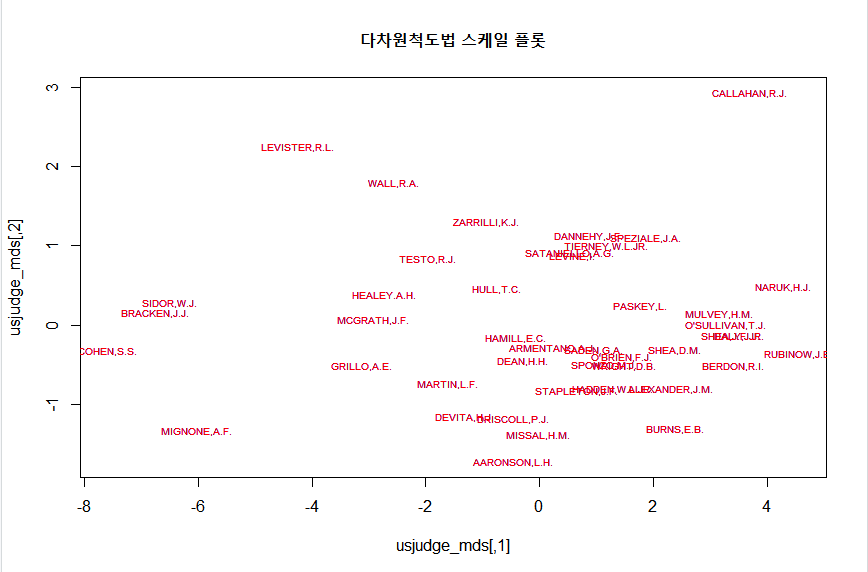
위의 결과를 보면, 어떤 판사들이 서로 비슷한 결과를 도출하는지, 타 판사들과는 다른 판결을 내리는지에 대해 생각해볼 수 있음.
- 비계량적 거리의 경우 유클리드언 거리 대신 cluster 패키지에 포함된 daisy 함수를 활용하여 계산할 수 있음. 이후 daisy함수를 통해 구한 거리행렬에 대해서는 MASS 패키지에 포함된 isoMDS 함수를 통해 다차원 척도법을 수행할 수 있음.
# case 2: 비계량적 거리 측정하기
# metric = gower를 측정하면, 계량, 비계량이 혼재된 데이터를 대상으로 거리를 측정할 수 있음.
# 이때 굳이 범주형 변수에 대해 factor 화를 취해주지 않아도 가능
mtcar_dist <- daisy(mtcars, metric = 'gower')
# 연속형/범주형 변수가 혼합된 데이터에 대한 거리행렬에 대해 다차원척도법을 수행하기 위해서는
# MASS 패키지에 있는 isoMDS()를 사용하면 됨
library(MASS)
mtcars_mds <- isoMDS(mtcar_dist)
str(mtcars_mds)
#위와 같이 그림을 통해 표현해볼 수 있음.
plot(mtcars_mds$points, type = 'n',
main = "다차원척도법 스케일 플롯") # 비어있는 플롯을 생성
text(mtcars_mds$points, rownames(mtcars), col = "red", cex = 0.6)
이후 이에 대해 plot을 그려보면 아래와 같음.
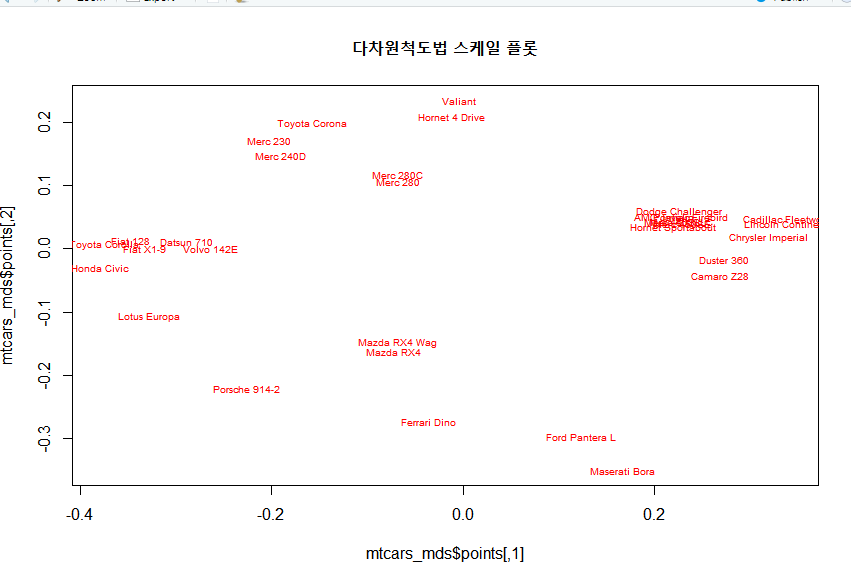
이를 통해 mtcars 데이터에 포함되어 있는 자동차 브랜드의 유사도를 확인해볼 수 있음.
전체 R 코드 정리
#데이터 불러오기
str(state.x77)
colnames(state.x77)
#pca 계산하기
pca <- prcomp(state.x77,
scale = T)
# PCA값 확인해보기
summary(pca)
#Scree Plot 시각화 하기
plot(pca,
type = "l",
col = "blue",
main = "Scree Plot")
#성분적재값 확인하기
round(pca$rotation, 3)
#성분 점수 계산하기
round(scale(state.x77) %*% pca$rotation, 3)
# 위와 같은 결과를 표출함
#round(pca$x, 3)
# 원하는 주성분의 갯수만큼만 잘라서 확인하기
round(pca$x[,c(1,2)], 3)
#주성분 분석 시각화하기
biplot(pca, main = "Biplot of PCA")
setwd("C:\\Users\\jupeter\\Downloads")
library(data.table)
#데이터 불러오기
survey<- fread("Factor-Hair-Revised.csv")
survey<-as.data.frame(survey)
#필요 패키지 불러오기
library(psych)
library(nFactors)
# 추출할 요인의 갯수 지정하기(fa.parallel 함수 활용)
fa.parallel(survey, #데이터 프레임
fm = "ml", # 최대우도법(Maximum Likelihood)를 토대로 요인의 갯수 지정
fa = "fa", # 요인분석(Factor Analysis)를 위한 고유값 표기
n.iter = 100 # 반복 횟수
)
# 4개를 사용하는 것을 추천
# 다른 방법(nFactor 패키지 활용)
nScree(survey)
# 4가지 방법론 중 3가지에서 4개의 Factor을 추천
# 다른 방법 eigen value 확인
eigen(cor(survey))
# eigen value가 1을 넘는 것이 4번째까지임.
#다만, 위의 결과는 보조지표일 뿐이며, 해석이 가능하도록 요인 갯수를 지정하는 것이 중요
#요인 분석 수행하기
fa <- factanal(survey, # 데이터
factor = 4, #요인의 갯수
scores = "regression") #요인점수 계산 시 사용할 방법 지정
#분석에 대한 결과 확인하기
fa
#요인 분석의 결과를 토대로 상관관계 파악하기
round(cor(survey) - #기존값에 대한 실제 상관관계 파악
(fa$loadings %*% t(fa$loadings) + #요인분석 결과의 loading과 요인분석 결과의 transpose의 행렬곱
diag(fa$uniquenesses)), #diag 함수는 주어진 벡터로 대각선을 채우고 나머지는 다 0으로 채움.
#이때 fa$uniqueness는 각 변수의 고유분산을 의미함
3) # 소수점 셋째 자리까지 표현
# Factor Plot 그리기
factor.plot(fa, labels = colnames(survey), pch = 20, pos= 4,
title= "Factor Plot")
#경로도 (Path Diagram 그리기)
library(semPlot)
semPaths(fa, what = "est", # 경로상에 요인적재값 나타내기
residuals = F, # 관측변수의 잔차 생략
cut = 0.3, # 0.3보다 작은 요인적재값은 그래프상에 나타나지 않도록 함
posCol = c("White", "darkgreen"), # 양수 관련
negCol = c("white", "red"), # 음수 관련
edge.label.cex = 0.75) # 요인적재값의 텍스트 크기
#다차원 척도법 MDS
# case 1 : 연속형 변수만 있는 경우
# 해당 데이터는 행의 이름에 판사의 이름이 들어가 있는 구조임(아래 plotting에서 사용)
str(USJudgeRatings)
# 연속형 변수이므로 우선 거리를 계산해야 함.
# 이후 계량 데이터로부터 생성된 근접행렬에 대해 적용할 수 있는 cmdscale()함수를 이용하여 MDS 수행
usjudge_dist <- dist(USJudgeRatings) # 유클리드 거리계산
usjudge_mds <- cmdscale(usjudge_dist)
# 이후 이에 대한 결과는 plot() 함수와 text() 함수를 이용하여 MDS 공간배치도로 나타낼 수 있음.
plot(usjudge_mds, type = 'n',
main = "다차원척도법 스케일 플롯") # 비어있는 플롯을 생성
text(usjudge_mds, rownames(USJudgeRatings), col = "red", cex = 0.6)
# case 2 : 연속형 + 범주형인 경우 거리 계산
# 데이터 불러오기
str(mtcars)
# 패키지 불러오기
library(cluster)
# 비계량적 거리 측정하기
# metric = gower를 측정하면, 계량, 비계량이 혼재된 데이터를 대상으로 거리를 측정할 수 있음.
# 이때 굳이 범주형 변수에 대해 factor 화를 취해주지 않아도 가능
mtcar_dist <- daisy(mtcars, metric = 'gower')
# 연속형/범주형 변수가 혼합된 데이터에 대한 거리행렬에 대해 다차원척도법을 수행하기 위해서는
# MASS 패키지에 있는 isoMDS()를 사용하면 됨
library(MASS)
mtcars_mds <- isoMDS(mtcar_dist)
str(mtcars_mds)
#위와 같이 그림을 통해 표현해볼 수 있음.
plot(mtcars_mds$points, type = 'n',
main = "다차원척도법 스케일 플롯") # 비어있는 플롯을 생성
text(mtcars_mds$points, rownames(mtcars), col = "red", cex = 0.6)
참고문헌
- 곽기영, R을 이용한 통계분석
- Stack overflow
- 곽기영 교수님의 유튜브, https://www.youtube.com/@kykwahk
'ADP 준비 > 머신러닝' 카테고리의 다른 글
| ADP 실기 준비 - 머신러닝 (1) 회귀분석 패키지/함수 정리 (2) | 2023.06.01 |
|---|---|
| ADP 20회 실기_ 머신러닝 파트 (0) | 2023.05.19 |
| 지도학습 > 의사결정나무 : CART, C5.0, C4.5, CHAID - R code (0) | 2023.02.01 |

댓글